What Percent of 80 is 60? Basic Math in English

Percentages appear everywhere in our daily lives—from discounts at stores to interest rates on loans, from test scores to statistical analyses. Understanding how to calculate them correctly isn't just an academic exercise; it's a practical skill that empowers informed decision-making. When faced with a question like "what percent of 80 is 60?" many people experience momentary confusion despite the apparent simplicity. This hesitation reveals a common gap in mathematical fluency that affects countless individuals across educational levels.

In this comprehensive guide, I'll break down the fundamental concepts behind percentage calculations, provide multiple solution methods for finding what percent of 80 is 60, and equip you with practical techniques to handle similar questions with confidence. By understanding the underlying principles rather than memorizing formulas, you'll develop the critical thinking skills necessary for mathematical reasoning in real-world situations.

Understanding the Basics of Percentages

Before diving into specific calculations, we must establish a solid foundation of what percentages actually represent. The term "percent" comes from the Latin "per centum," meaning "by the hundred." At its core, a percentage is simply a fraction with 100 as the denominator.

When we say "75 percent" (written as 75%), we are effectively saying "75 out of 100" or "75/100" or "0.75" in decimal form. This fraction represents a ratio that can be applied to any quantity. Percentages provide us with a standardized way to express proportions, making comparisons more intuitive across different contexts and magnitudes.

The fundamental relationship can be expressed through this equation:

Percentage = (Part ÷ Whole) × 100%

This equation captures the essential relationship between a part and a whole, converting their ratio into a percentage value. Understanding this relationship is the foundation for all percentage calculations.

What Percent of 80 is 60? Step-by-Step Solution

When analyzing the question "what percent of 80 is 60?", we need to identify the components clearly:

60 is the part
80 is the whole
We need to find the percentage

Method 1: Using the Percentage Formula

The most direct approach uses the fundamental percentage formula:

Percentage = (Part ÷ Whole) × 100%

Substituting the values: Percentage = (60 ÷ 80) × 100% Percentage = 0.75 × 100% Percentage = 75%

Therefore, 60 is 75% of 80.

This method works universally for all percentage calculations when you know the part and the whole. The division operation gives us the decimal representation of the proportion, which we then multiply by 100 to convert to a percentage.

Method 2: Setting Up a Proportion

Another approach involves setting up a proportion using the fact that percentages are based on 100:

x/100 = 60/80

In this equation, x represents the percentage we're looking for. We can cross-multiply to solve:

x × 80 = 60 × 100 x × 80 = 6,000 x = 6,000 ÷ 80 x = 75

So, again, 60 is 75% of 80.

This proportional method reinforces the conceptual understanding of percentages as "parts per hundred" and provides an alternative solution path that some may find more intuitive, especially those who are comfortable with proportional reasoning.

Method 3: Using the Decimal Approach

We can also solve this by converting directly to a decimal:

Divide the part by the whole: 60 ÷ 80 = 0.75
Convert the decimal to a percentage by multiplying by 100: 0.75 × 100 = 75%

This method highlights the relationship between decimals and percentages, reinforcing that a percentage is simply a decimal multiplied by 100.

Understanding the Equation for Percentage Calculations

The equation to find what percent one number is of another can be written as:

P% of W = V

Where:

P is the percentage we're trying to find
W is the whole amount (in our case, 80)
V is the value we're comparing (in our case, 60)

To solve for P, we rearrange the equation:

P = (V ÷ W) × 100

This equation forms the foundation of all percentage calculations of this type. In our specific example:

P = (60 ÷ 80) × 100 = 75

Therefore, 60 is 75% of 80.

Understanding this equation allows you to tackle any similar problem by simply substituting the appropriate values for V and W.

Real-World Applications of This Percentage Calculation

Understanding the percentage relationship between 60 and 80 has practical applications across various domains:

Academic Performance

If a student scored 60 points on an 80-point exam, they achieved 75%. This immediate conversion allows both the student and instructor to gauge performance on a standardized scale, regardless of the total possible points on the assessment.

Financial Analysis

If a business generated $60,000 in revenue against a projected $80,000, they achieved 75% of their target. This percentage provides immediate insight into performance relative to expectations, allowing for more meaningful assessment than the raw numbers alone.

Health and Fitness

If someone completed 60 minutes of a planned 80-minute workout, they completed 75% of their intended exercise session. This percentage helps track adherence to fitness plans and progress toward goals.

Resource Utilization

If 60 out of 80 available resources are being utilized, the utilization rate is 75%. This metric helps organizations identify efficiency opportunities and optimize resource allocation.

These examples demonstrate how the simple calculation of what percent of 80 is 60 translates into meaningful insights across diverse contexts. The ability to quickly determine and interpret these percentages enhances decision-making in both personal and professional settings.

Common Mistakes When Calculating Percentages

Even with seemingly straightforward calculations like determining what percent of 80 is 60, people frequently make errors that lead to incorrect results. Recognizing these common pitfalls can help avoid them:

Inverting the Numerator and Denominator

A frequent error is dividing the whole by the part instead of the part by the whole. If someone calculated 80 ÷ 60 instead of 60 ÷ 80, they would incorrectly get 1.33 or 133% instead of 75%.

This error fundamentally misrepresents the relationship between the numbers. Remember: the part (what we're finding the percentage of) always goes in the numerator, and the whole (what we're comparing to) goes in the denominator.

Forgetting to Multiply by 100

Another common mistake is stopping after dividing the part by the whole, giving the answer as 0.75 instead of 75%. While 0.75 is the correct decimal representation, it must be multiplied by 100 to convert to a percentage.

This error stems from conflating decimals with percentages. They represent the same proportion but in different forms—decimals as a fraction of 1, percentages as a fraction of 100.

Misinterpreting the Question

Some people misunderstand what the question is asking. "What percent of 80 is 60?" asks for the percentage that 60 represents of 80, not the difference between them or how much larger one is than the other.

This confusion often results from imprecise language understanding or rushing through the problem without clearly identifying what's being asked.

Rounding Errors

Premature rounding during intermediate steps can lead to inaccurate final answers, especially in more complex percentage problems. Always perform all calculations before rounding to ensure accuracy.

By being aware of these common mistakes, you can approach percentage calculations more methodically, double-checking your work against these known error patterns.

Different Types of Percentage Questions

Percentage questions come in various forms, each requiring a slightly different approach. Understanding these variations helps identify the correct method for each scenario:

Finding the Percentage (our current example)

Question: What percent of 80 is 60? Formula: Percentage = (Part ÷ Whole) × 100% Solution: (60 ÷ 80) × 100% = 75%

Finding the Part

Question: What is 30% of 250? Formula: Part = (Percentage ÷ 100) × Whole Solution: (30 ÷ 100) × 250 = 0.3 × 250 = 75

Finding the Whole

Question: 42 is 35% of what number? Formula: Whole = Part ÷ (Percentage ÷ 100) Solution: 42 ÷ (35 ÷ 100) = 42 ÷ 0.35 = 120

Percentage Increase or Decrease

Question: If a price increases from $80 to $100, what is the percentage increase? Formula: Percentage Change = ((New Value - Original Value) ÷ Original Value) × 100% Solution: ((100 - 80) ÷ 80) × 100% = (20 ÷ 80) × 100% = 25%

Each type requires identifying the correct variables and applying the appropriate formula. Being able to recognize which type of percentage question you're facing is the first step toward arriving at the correct solution.

The Relationship Between Fractions, Decimals, and Percentages

Percentages exist within a broader numerical ecosystem, closely related to fractions and decimals. Understanding these relationships enhances overall mathematical fluency:

Fractions to Percentages

To convert a fraction to a percentage:

Divide the numerator by the denominator to get a decimal
Multiply the decimal by 100 and add the % symbol

Example: 3/4 = 0.75 = 75%

In our case, 60/80 = 3/4 = 75%

Decimals to Percentages

To convert a decimal to a percentage:

Multiply the decimal by 100
Add the % symbol

Example: 0.35 = 35%

In our case, 60 ÷ 80 = 0.75 = 75%

Percentages to Fractions

To convert a percentage to a fraction:

Remove the % symbol and place the number over 100
Simplify the fraction if possible

Example: 75% = 75/100 = 3/4

Percentages to Decimals

To convert a percentage to a decimal:

Remove the % symbol
Divide by 100

Example: 75% = 75 ÷ 100 = 0.75

These interconversions demonstrate that percentages, fractions, and decimals are simply different representations of the same proportional relationships. Mastering these conversions provides multiple approaches to solve percentage problems and enhances numerical flexibility.

The Importance of Percentage Calculations in Data Literacy

In today's data-driven world, percentage calculations form a cornerstone of data literacy. The ability to calculate and interpret percentages correctly enables:

Critical Evaluation of Statistical Claims

When media reports claim "75% increase in demand," understanding percentage calculations allows you to assess whether this represents a significant change or if the baseline was so small that the percentage seems misleadingly large.

Financial Decision-Making

From evaluating investment returns to understanding loan interest rates, percentage calculations directly impact financial well-being. The difference between an investment yielding 5% versus 7% annual returns becomes substantial over decades.

Scientific Literacy

Scientific literature frequently presents findings as percentage changes or proportions. Understanding these representations is essential for interpreting research results accurately.

Business Analysis

Business metrics often use percentages to standardize comparisons across different scales—profit margins, growth rates, market share, and conversion rates all rely on percentage calculations.

Developing comfort with percentage calculations like determining what percent of 80 is 60 builds the foundation for these broader applications, contributing to overall numerical confidence and analytical capabilities.

Mental Math Strategies for Percentage Calculations

While formal methods are important for understanding, developing mental math strategies for percentages enhances practical application:

Using Fraction Equivalents

Some percentages have simple fraction equivalents that make calculations easier:

75% = 3/4, so to find 75% of a number, find 3/4 of it
For our example: 3/4 of 80 = 3 × 80 ÷ 4 = 240 ÷ 4 = 60

Alternatively, you can think: 75% = 50% + 25% = 1/2 + 1/4

50% of 80 = 40
25% of 80 = 20
75% of 80 = 40 + 20 = 60

Benchmark Percentages

Use common percentages as anchors:

10% is easily found by moving the decimal point
5% is half of 10%
1% is 1/100 of the number

For our example:

10% of 80 = 8
50% of 80 = 40
25% of 80 = 20
75% = 50% + 25%, so 75% of 80 = 40 + 20 = 60

Working Backward

Sometimes it's easier to start with the percentage and work backward. If 60 is 75% of 80, then 80 must be 100% and each 1% would be 0.8. So 75% would be 75 × 0.8 = 60.

These mental strategies provide practical shortcuts that can be applied in daily situations where calculating percentages is necessary but a calculator isn't available.

Advanced Percentage Concepts

Beyond basic calculations, understanding more advanced percentage concepts extends your mathematical toolkit:

Compounding Percentages

When percentages are applied sequentially, they don't simply add. For example, a 10% increase followed by another 10% increase doesn't result in a 20% increase overall, but rather:

Original amount: x
After first 10% increase: 1.1x
After second 10% increase: 1.1 × 1.1x = 1.21x
This represents a 21% total increase

Percentage Points vs. Percentages

A common source of confusion is the difference between percentage points and percentages:

If an interest rate increases from 5% to 7%, that's a 2 percentage point increase
But it's a 40% increase in the rate itself (7 is 40% more than 5)

Understanding this distinction is crucial for interpreting economic and statistical reports accurately.

Relative vs. Absolute Percentage Changes

The base used for calculating a percentage change matters:

If a value increases from 80 to 100, that's a 25% increase
If it then decreases from 100 to 80, that's a 20% decrease

Despite returning to the original value, the percentage changes are not equal because they reference different base values.

These advanced concepts highlight that percentages, while seemingly straightforward, contain subtleties that require careful consideration in complex situations.

Using Technology for Percentage Calculations

While understanding manual calculation methods is essential, leveraging technology can enhance efficiency and accuracy:

Calculator Methods

Most calculators have percentage functions that streamline calculations:

To find what percent of 80 is 60:
Basic calculator: 60 ÷ 80 × 100 = 75
Scientific calculator: Often has a dedicated % button that can be used in various percentage calculations

Spreadsheet Formulas

Spreadsheet applications offer powerful tools for percentage calculations:

In Excel/Google Sheets: =60/80 formatted as a percentage gives 75%
More complex percentage calculations can be automated using built-in functions

Mobile Apps

Numerous mobile applications specialize in percentage calculations, offering:

Dedicated interfaces for different types of percentage problems
Step-by-step solutions for educational purposes
Real-world applications like tip calculators, discount calculators, etc.

While technology provides convenience, the fundamental understanding developed through manual methods ensures you can verify results and apply the concepts correctly in various contexts.

Cultural and Historical Context of Percentages

The concept of percentages has evolved over centuries, reflecting broader mathematical and commercial developments:

Historical Development

The use of hundredths dates back to ancient Roman times, but the modern percentage symbol (%) emerged much later, likely evolving from the Italian term "per cento" (per hundred). The symbol itself appears to be a evolution of the notation "pc" with the p and c eventually merging into the current % symbol.

Percentages Across Disciplines

Different fields developed specialized percentage applications:

Commerce: Interest calculations, profit margins
Statistics: Probability expressed as percentages
Science: Concentration levels, efficiency metrics
Government: Tax rates, demographic analyses

Understanding this historical and disciplinary context enriches appreciation for percentage calculations beyond their mere computational value.

Learn Any Language with Kylian AI

Private language lessons are expensive. Paying between 15 and 50 euros per lesson isn’t realistic for most people—especially when dozens of sessions are needed to see real progress.

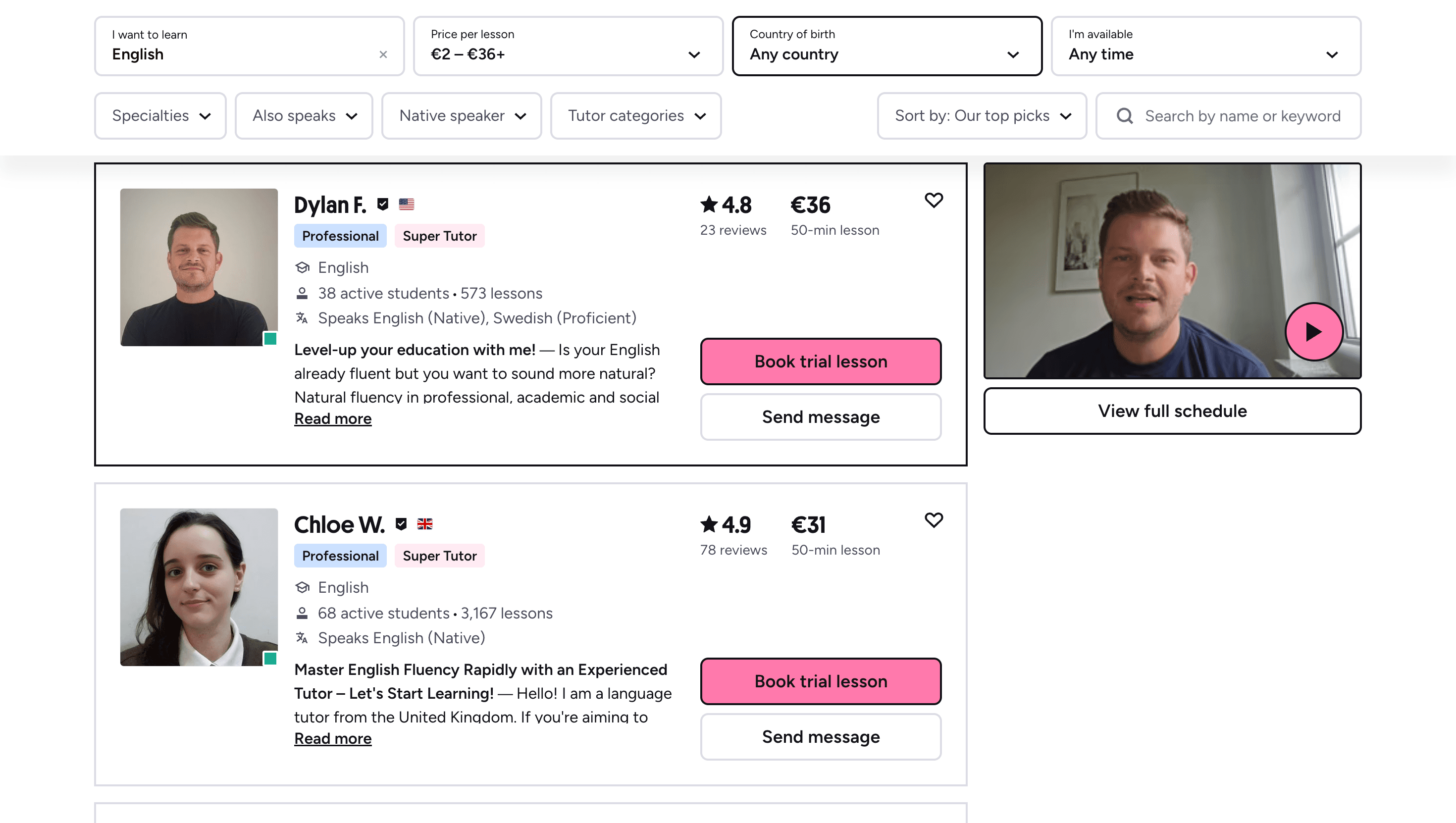
Many learners give up on language learning due to these high costs, missing out on valuable professional and personal opportunities.

That’s why we created Kylian: to make language learning accessible to everyone and help people master a foreign language without breaking the bank.

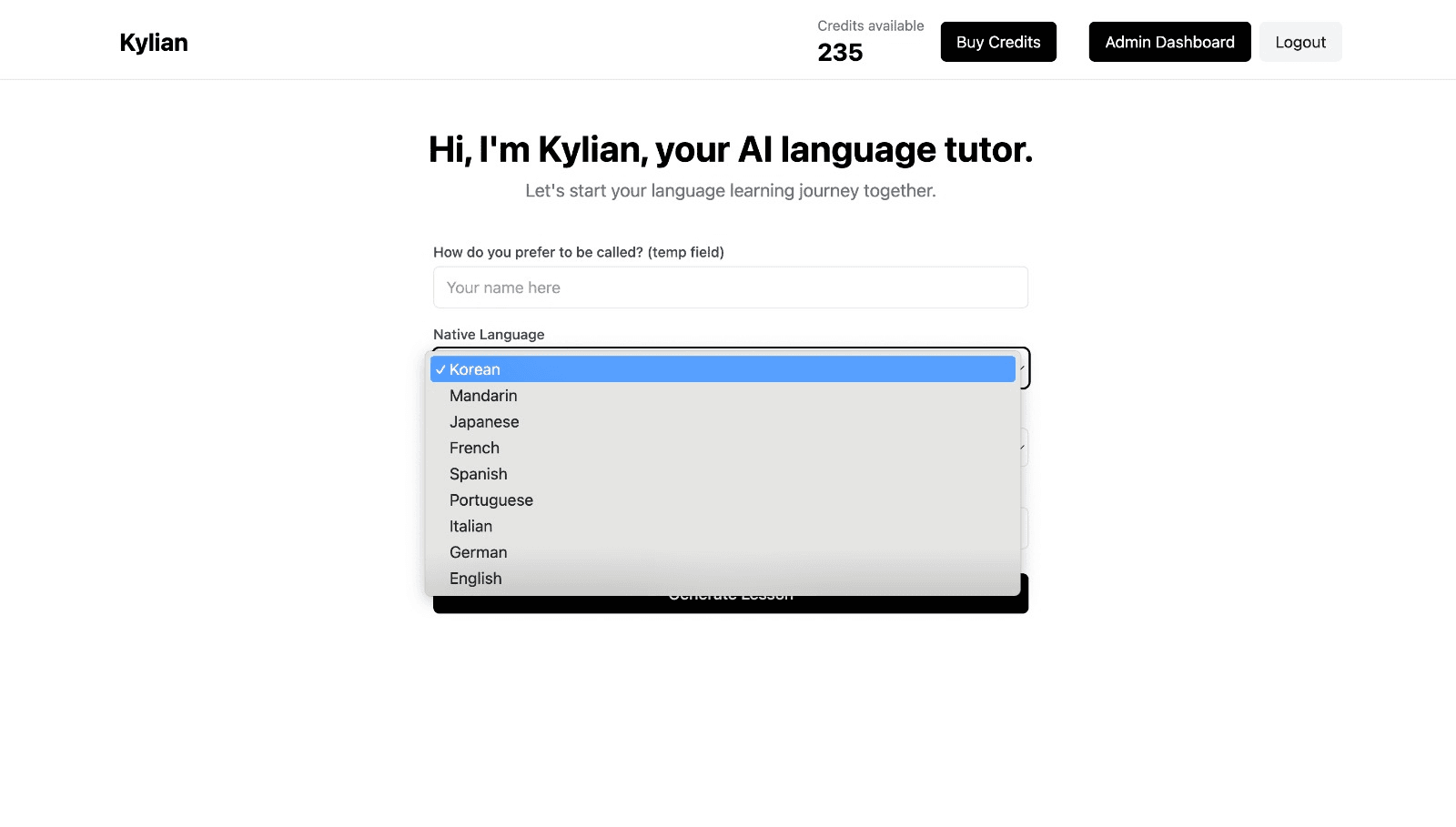
To get started, just tell Kylian which language you want to learn and what your native language is

Tired of teachers who don’t understand your specific struggles as a French speaker? Kylian’s advantage lies in its ability to teach any language using your native tongue as the foundation.

Unlike generic apps that offer the same content to everyone, Kylian explains concepts in your native language (French) and switches to the target language when necessary—perfectly adapting to your level and needs.

This personalization removes the frustration and confusion that are so common in traditional language learning.

Choose a specific topic you want to learn

Frustrated by language lessons that never cover exactly what you need? Kylian can teach you any aspect of a language—from pronunciation to advanced grammar—by focusing on your specific goals.

Avoid vague requests like “How can I improve my accent?” and be precise: “How do I pronounce the R like a native English speaker?” or “How do I conjugate the verb ‘to be’ in the present tense?”

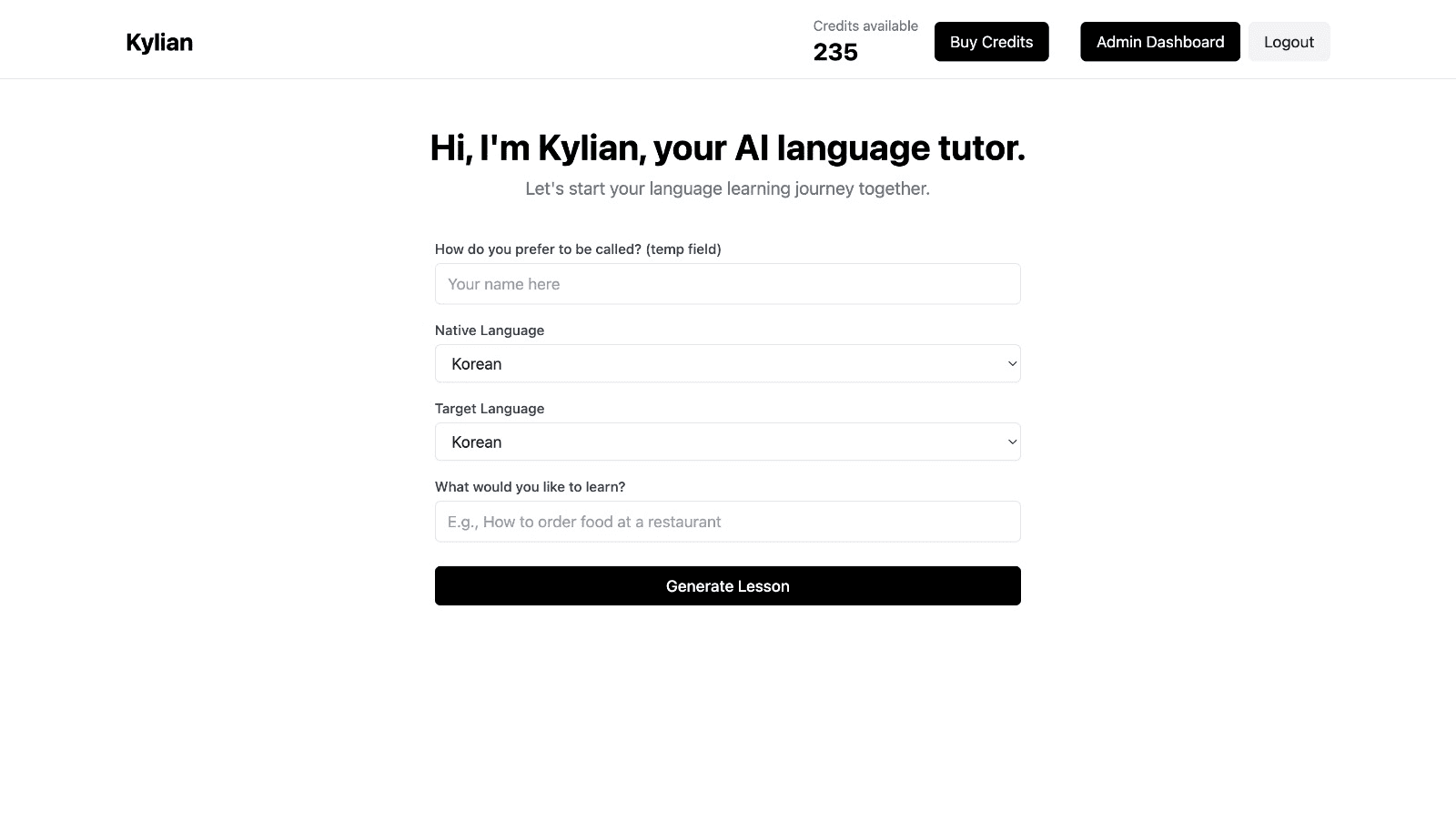
With Kylian, you’ll never again pay for irrelevant content or feel embarrassed asking “too basic” questions to a teacher. Your learning plan is entirely personalized.

Once you’ve chosen your topic, just hit the “Generate a Lesson” button, and within seconds, you’ll get a lesson designed exclusively for you.

Join the room to begin your lesson

The session feels like a one-on-one language class with a human tutor—but without the high price or time constraints.

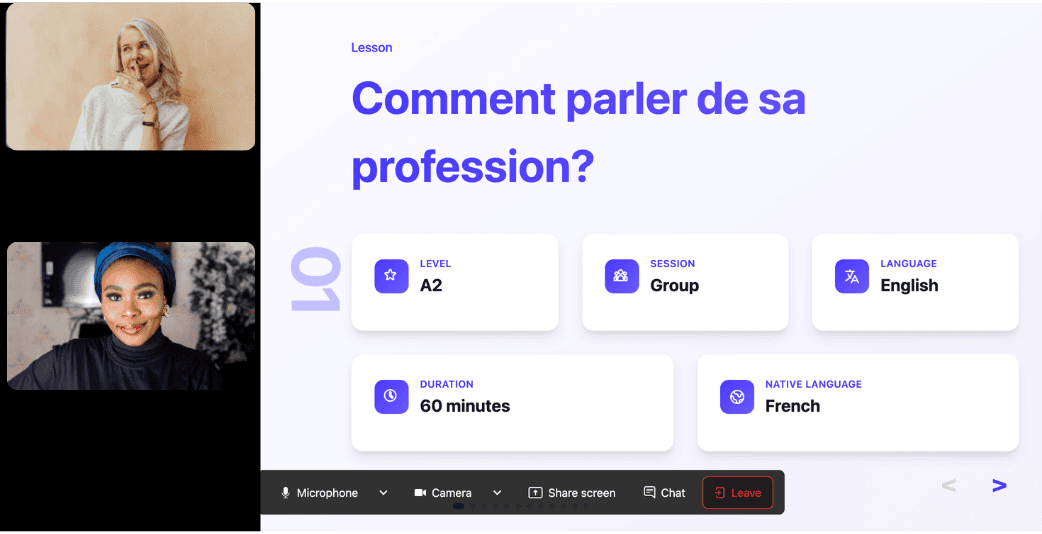
In a 25-minute lesson, Kylian teaches exactly what you need to know about your chosen topic: the nuances that textbooks never explain, key cultural differences between French and your target language, grammar rules, and much more.

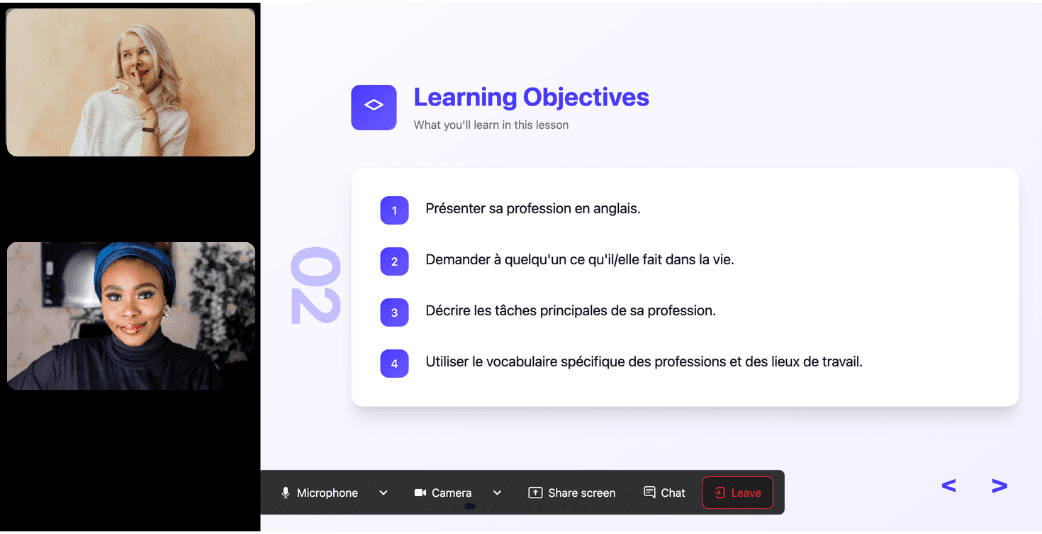
Ever felt frustrated trying to keep up with a native-speaking teacher, or embarrassed to ask for something to be repeated? With Kylian, that problem disappears. It switches intelligently between French and the target language depending on your level, helping you understand every concept at your own pace.

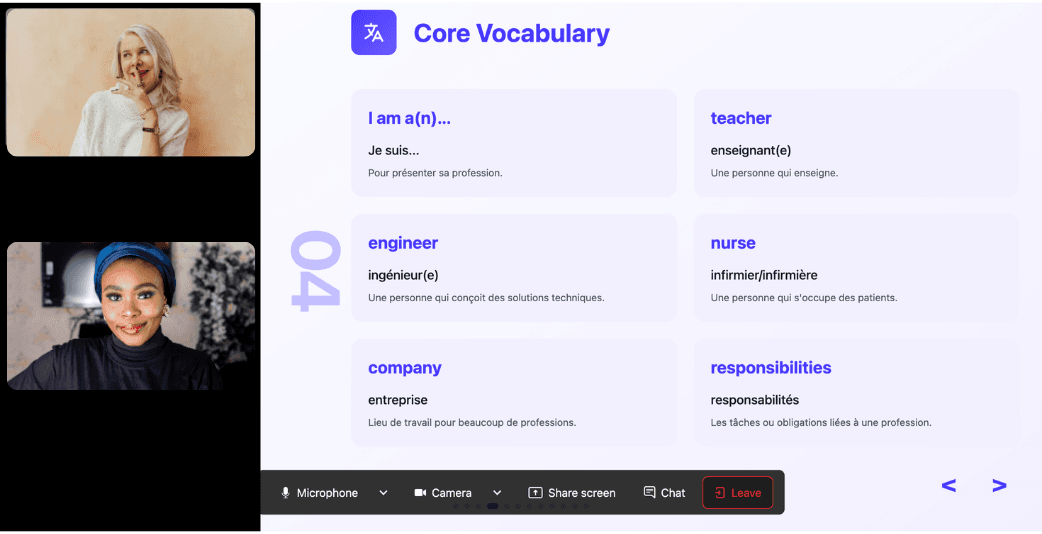
During the lesson, Kylian uses role-plays, real-life examples, and adapts to your learning style. Didn’t understand something? No problem—you can pause Kylian anytime to ask for clarification, without fear of being judged.

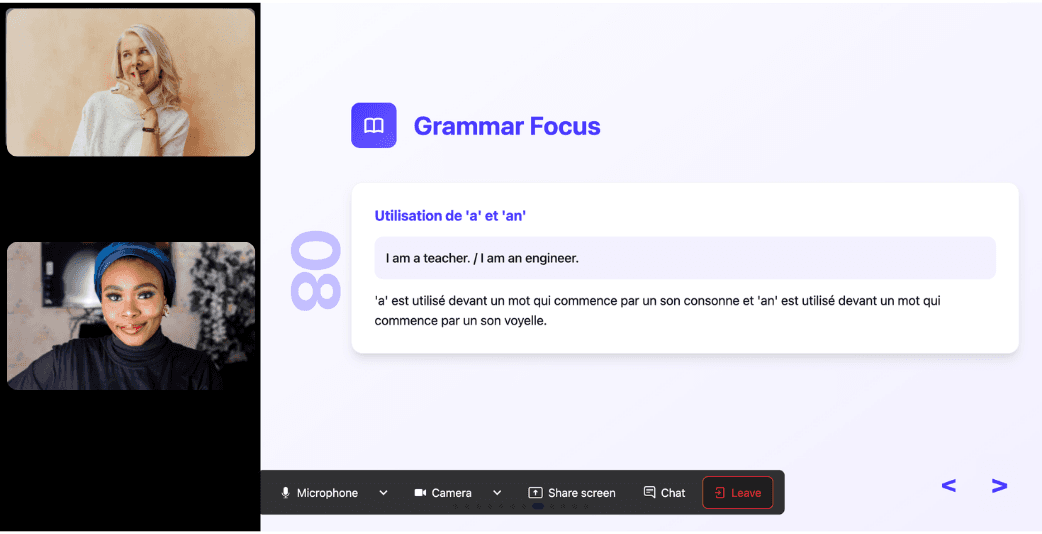
Ask all the questions you want, repeat sections if needed, and customize your learning experience in ways traditional teachers and generic apps simply can’t match.

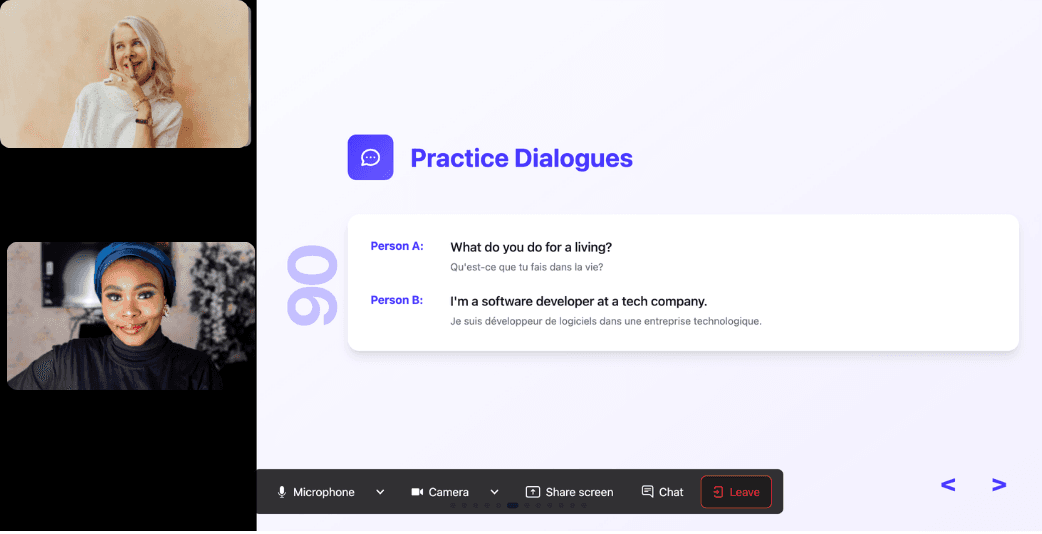
With 24/7 access at a fraction of the cost of private lessons, Kylian removes all the barriers that have kept you from mastering the language you’ve always wanted to learn.

Take your free lesson with Kylian today.