60+ Essential Math Vocabulary Words in English

Mathematics transcends cultural and linguistic boundaries, but mastering math terminology in English is crucial for academic success, professional growth, and effective communication in educational settings. This comprehensive guide presents 60+ essential mathematical terms that will strengthen your English proficiency in mathematics and help you excel in exams and classroom discussions.

Why Mathematical Vocabulary Matters

The language of mathematics is precise and universal. However, when studying or working in English-speaking environments, understanding specific mathematical terminology becomes indispensable. Without proper vocabulary, even those with strong mathematical abilities may struggle to:

Comprehend exam questions correctly

Articulate mathematical concepts during class discussions

Follow lectures and instructional materials

Communicate effectively with teachers and peers

A strong command of mathematical vocabulary in English serves as the foundation for academic achievement across various disciplines including science, engineering, economics, and computer science.

Core Mathematical Operations: The Building Blocks

The most fundamental mathematical vocabulary revolves around the four basic operations. These terms form the cornerstone of arithmetic and are essential for solving even the most basic mathematical problems:

Addition (+) – The process of combining numbers to find their total or sum. Example: 5 + 7 = 12

Subtraction (–) – The process of removing one number from another to find their difference. Example: 10 – 3 = 7

Multiplication (×) – The process of repeated addition, finding the product of numbers. Example: 4 × 6 = 24

Division (÷) – The process of splitting a quantity into equal parts to find the quotient. Example: 20 ÷ 5 = 4

Understanding these core operations is the gateway to more advanced mathematical concepts. Each operation has associated terminology that appears consistently across different branches of mathematics.

Essential Arithmetic Terminology

Arithmetic forms the foundation of mathematics and encompasses the study of numbers and basic operations. Mastering these terms is critical for building mathematical confidence:

Sum – The result of adding two or more numbers. Example: In 3 + 4 = 7, the sum is 7.

Difference – The result of subtracting one number from another. Example: In 9 – 5 = 4, the difference is 4.

Product – The result of multiplying two or more numbers. Example: In 6 × 3 = 18, the product is 18.

Quotient – The result of dividing one number by another. Example: In 15 ÷ 3 = 5, the quotient is 5.

Factor – A number that divides another number exactly without a remainder. Example: The factors of 12 are 1, 2, 3, 4, 6, and 12.

Multiple – A number that is the product of a given number and an integer. Example: The multiples of 3 are 3, 6, 9, 12, etc.

Dividend – The number being divided in a division problem. Example: In 20 ÷ 4 = 5, the dividend is 20.

Divisor – The number that divides the dividend. Example: In 20 ÷ 4 = 5, the divisor is 4.

Remainder – The amount left over when one number doesn't divide exactly into another. Example: In 17 ÷ 5 = 3 with remainder 2, the remainder is 2.

Integer – A whole number that can be positive, negative, or zero. Example: -3, -2, -1, 0, 1, 2, 3.

Key Algebraic Concepts and Terminology

Algebra extends beyond arithmetic by introducing variables and studying the relationships between quantities. These essential algebraic terms will help you navigate equations and expressions with confidence:

Equation – A mathematical statement showing that two expressions are equal, typically containing an equals sign (=). Example: 2x + 3 = 11

Expression – A combination of numbers, variables, and operations without an equals sign. Example: 3y² + 4y - 7

Variable – A symbol (usually a letter) that represents an unknown value or one that can change. Example: In the expression 5x + 2, x is the variable.

Coefficient – The numerical factor in a term with a variable. Example: In 7y, the coefficient is 7.

Function – A relation that assigns exactly one output to each input. Example: f(x) = x² + 3

Linear equation – An equation whose graph is a straight line, typically in the form ax + b = c. Example: 2x + 5 = 13

Quadratic equation – An equation containing a variable raised to the second power, with the form ax² + bx + c = 0. Example: x² - 5x + 6 = 0

Solution – The value(s) that satisfy an equation. Example: The solution to x + 4 = 10 is x = 6.

Constant – A fixed value that doesn't change. Example: In y = 3x + 5, the constant is 5.

Term – A single number, variable, or the product of a number and variable(s). Example: In 3x² + 4y - 7, the terms are 3x², 4y, and -7.

Fundamental Geometric Terms

Geometry studies shapes, sizes, and properties of space. These geometric terms are essential for spatial reasoning and measurement:

Point – An exact location in space, having no size or dimension.

Line – A straight path that extends infinitely in both directions.

Ray – A portion of a line with one endpoint that extends infinitely in one direction.

Angle – The figure formed by two rays sharing a common endpoint (vertex). Example: Right angle (90°), acute angle (<90°), obtuse angle (>90°).

Triangle – A polygon with three sides and three angles. Example: Equilateral, isosceles, and scalene triangles.

Quadrilateral – A polygon with four sides and four angles. Example: Square, rectangle, rhombus, parallelogram.

Circle – A shape consisting of all points at a fixed distance (radius) from a central point.

Perimeter – The distance around a two-dimensional shape. Example: The perimeter of a square with 5-cm sides is 20 cm.

Area – The amount of space inside a two-dimensional shape. Example: The area of a rectangle with length 6 cm and width 4 cm is 24 cm².

Volume – The amount of space occupied by a three-dimensional object. Example: The volume of a cube with 3-cm edges is 27 cm³.

Essential Calculus Terminology

Calculus explores the concepts of change and motion through the study of derivatives, integrals, and limits. These terms are crucial for advanced mathematics:

Derivative – The rate at which a function changes at a specific point. Example: The derivative of f(x) = x² is f'(x) = 2x.

Integral – The accumulation of quantities, often represented as the area under a curve. Example: The integral of f(x) = 2x is F(x) = x² + C.

Limit – The value that a function approaches as the input approaches a certain value. Example: The limit of (x² - 1)/(x - 1) as x approaches 1 is 2.

Continuity – A property of functions where small changes in input result in small changes in output without breaks or jumps.

Differential equation – An equation that relates a function with its derivatives. Example: dy/dx = 2x + 3

Statistical and Probability Terms

Statistics and probability are increasingly important in data-driven fields. These terms are essential for analyzing data and making predictions:

Mean – The average of a set of numbers, calculated by dividing the sum by the count. Example: The mean of 3, 7, and 11 is (3+7+11)/3 = 7.

Median – The middle value in an ordered list of numbers. Example: The median of 2, 5, 7, 9, 11 is 7.

Mode – The most frequently occurring value in a set. Example: The mode of 2, 3, 3, 5, 7, 3 is 3.

Range – The difference between the maximum and minimum values in a data set. Example: The range of 4, 7, 10, 12, 15 is 15 - 4 = 11.

Probability – A measure of the likelihood of an event occurring, expressed as a number between 0 and 1. Example: The probability of rolling a 6 on a fair die is 1/6.

Standard deviation – A measure of the amount of variation or dispersion in a set of values. A low standard deviation indicates values are close to the mean.

Mathematical Symbols and Notations

Mathematical symbols are the universal language that transcends spoken words. Understanding these symbols is crucial for interpreting mathematical expressions:

= (equals) – Indicates that the values on either side are the same. Example: 7 + 3 = 10

≠ (not equal to) – Indicates that the values on either side are different. Example: 5 ≠ 8

< (less than) – Indicates that the value on the left is smaller than the value on the right. Example: 3 < 7

> (greater than) – Indicates that the value on the left is larger than the value on the right. Example: 9 > 4

≤ (less than or equal to) – Indicates that the value on the left is smaller than or equal to the value on the right. Example: x ≤ 5

≥ (greater than or equal to) – Indicates that the value on the left is larger than or equal to the value on the right. Example: y ≥ 10

π (pi) – The ratio of a circle's circumference to its diameter, approximately 3.14159.

∑ (sigma) – Used to denote summation. Example: ∑(i=1 to 4) i = 1+2+3+4 = 10

√ (square root) – Indicates the square root operation. Example: √9 = 3

|x| (absolute value) – Represents the distance of x from zero without regard to direction. Example: |−5| = 5

Number Systems and Classifications

Understanding different types of numbers and their classifications is fundamental to mathematical reasoning:

Natural numbers – The counting numbers: 1, 2, 3, 4, ...

Whole numbers – The natural numbers including zero: 0, 1, 2, 3, ...

Integers – Whole numbers and their negatives: ..., -3, -2, -1, 0, 1, 2, 3, ...

Rational numbers – Numbers that can be expressed as a fraction p/q, where p and q are integers and q ≠ 0. Example: 3/4, -2/5

Irrational numbers – Numbers that cannot be expressed as a simple fraction. Example: √2, π

Real numbers – The set of all rational and irrational numbers.

Prime number – A natural number greater than 1 that has no positive divisors other than 1 and itself. Example: 2, 3, 5, 7, 11

Composite number – A natural number greater than 1 that has positive divisors other than 1 and itself. Example: 4, 6, 8, 9, 10

Applied Mathematics Terminology

These terms bridge theoretical mathematics with real-world applications:

Percentage – A ratio expressed as a fraction of 100. Example: 25% means 25/100 or 0.25.

Ratio – A comparison of two or more numbers, indicating their relative sizes. Example: The ratio of 3 to 4 is written as 3:4.

Proportion – An equation stating that two ratios are equal. Example: 2/3 = 8/12

Scale – A ratio that compares a measurement on a model or drawing to the actual measurement. Example: A map scale of 1:100,000 means 1 cm on the map represents 100,000 cm in reality.

Vector – A quantity that has both magnitude and direction. Example: Velocity, which includes both speed and direction.

Why This Vocabulary Matters in Real-World Applications

The mathematical vocabulary presented here extends far beyond the classroom. These terms appear in diverse professional contexts:

Scientists use statistical terminology to analyze experimental data

Engineers apply geometric and calculus concepts to design structures

Economists use algebraic models to predict market trends

Computer programmers implement mathematical algorithms using these foundational terms

Financial analysts employ probability and statistics to assess investment risks

Mastering these terms in English facilitates professional communication and collaboration in global contexts where English serves as the primary language of exchange.

Strategies for Learning Mathematical Vocabulary

Learning mathematical vocabulary in English requires deliberate practice:

Create flashcards with the term on one side and both the definition and an example on the other

Use the terms in context by working through problems that specifically employ that vocabulary

Explain concepts to others using the proper terminology

Read mathematical texts in English to see how terms are used in context

Practice regularly to maintain recall and fluency

Learn Any Language with Kylian AI

Private language lessons are expensive. Paying between 15 and 50 euros per lesson isn’t realistic for most people—especially when dozens of sessions are needed to see real progress.

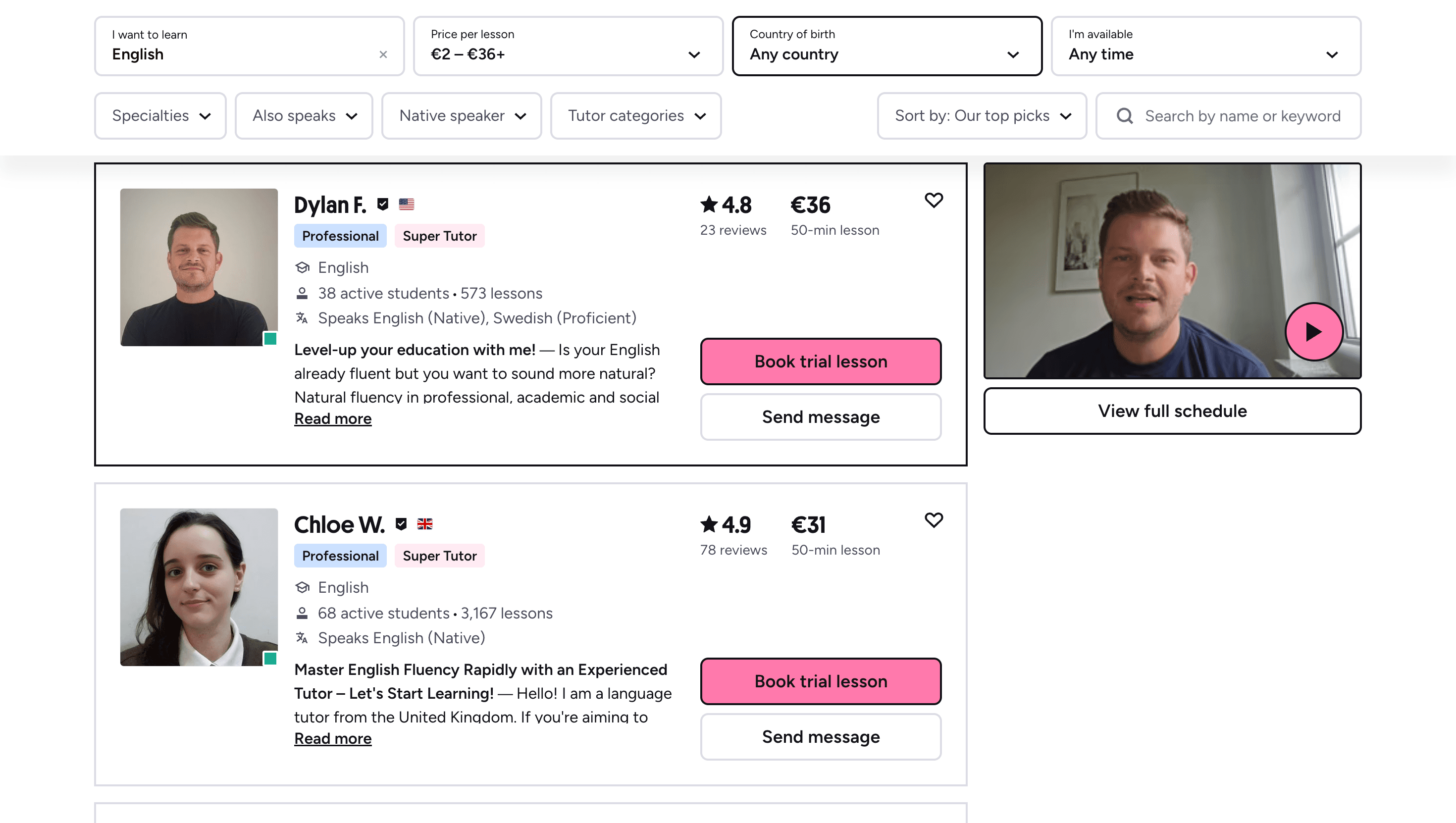
Many learners give up on language learning due to these high costs, missing out on valuable professional and personal opportunities.

That’s why we created Kylian: to make language learning accessible to everyone and help people master a foreign language without breaking the bank.

To get started, just tell Kylian which language you want to learn and what your native language is

Tired of teachers who don’t understand your specific struggles as a French speaker? Kylian’s advantage lies in its ability to teach any language using your native tongue as the foundation.

Unlike generic apps that offer the same content to everyone, Kylian explains concepts in your native language (French) and switches to the target language when necessary—perfectly adapting to your level and needs.

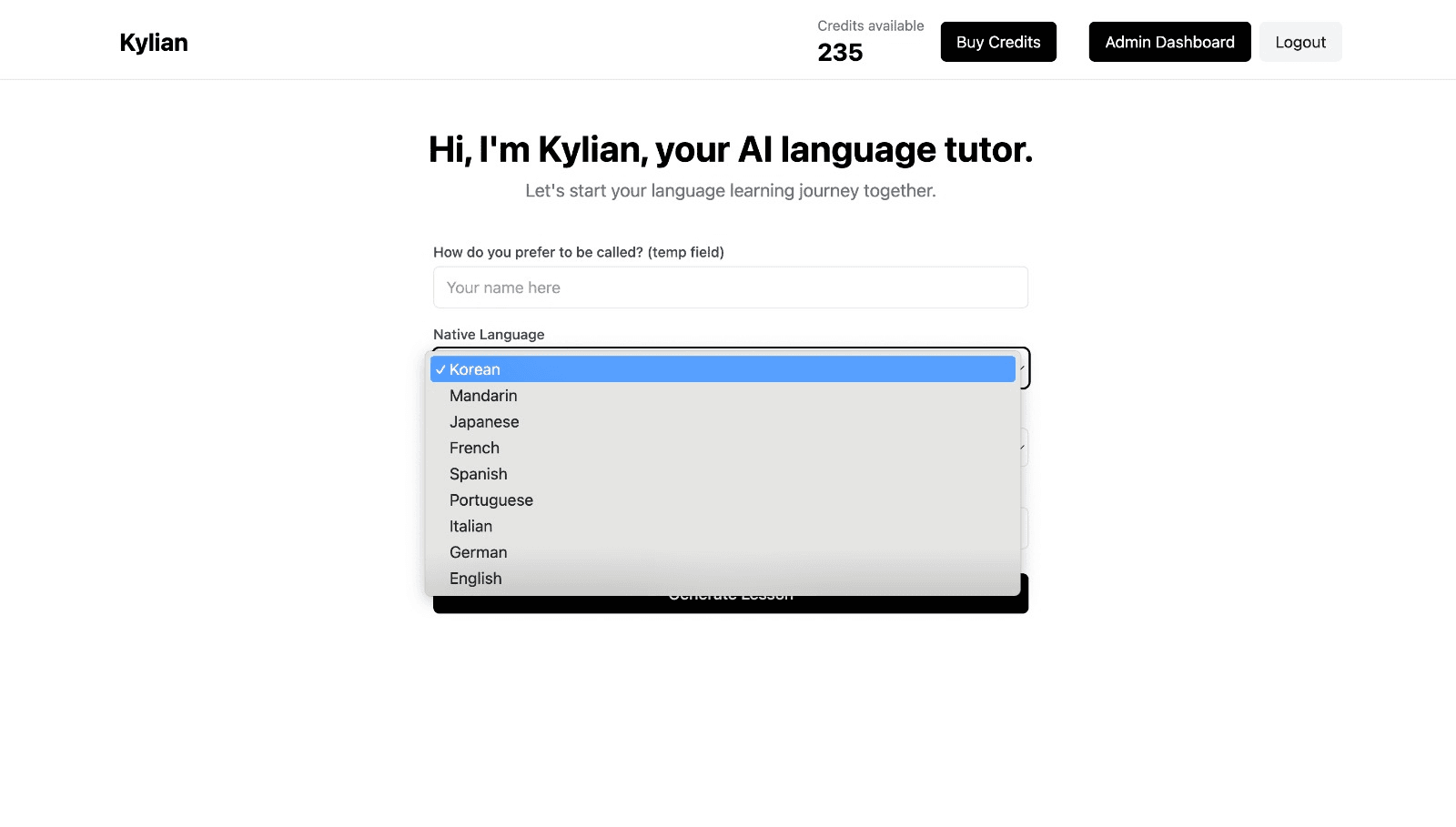
This personalization removes the frustration and confusion that are so common in traditional language learning.

Choose a specific topic you want to learn

Frustrated by language lessons that never cover exactly what you need? Kylian can teach you any aspect of a language—from pronunciation to advanced grammar—by focusing on your specific goals.

Avoid vague requests like “How can I improve my accent?” and be precise: “How do I pronounce the R like a native English speaker?” or “How do I conjugate the verb ‘to be’ in the present tense?”

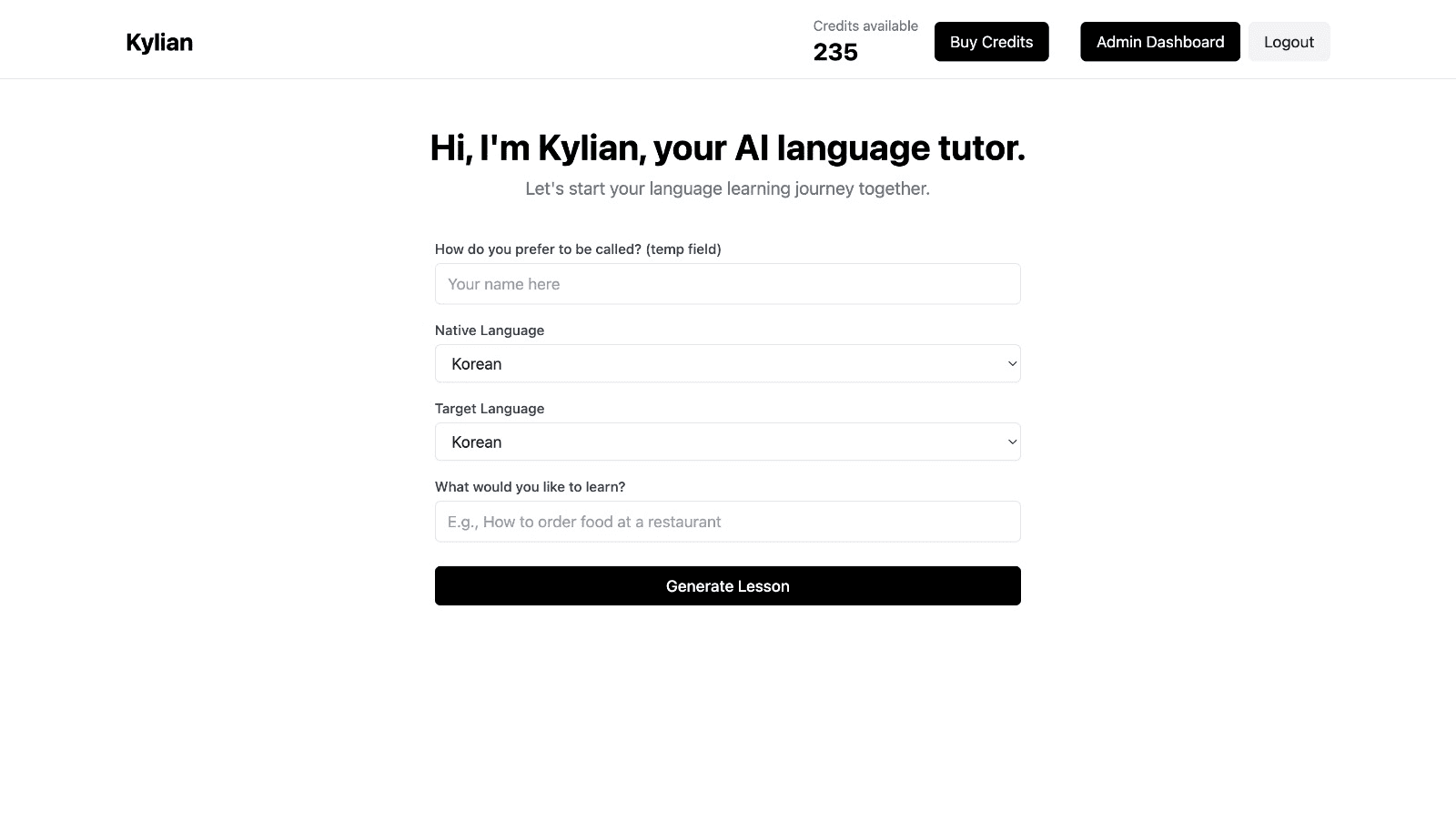
With Kylian, you’ll never again pay for irrelevant content or feel embarrassed asking “too basic” questions to a teacher. Your learning plan is entirely personalized.

Once you’ve chosen your topic, just hit the “Generate a Lesson” button, and within seconds, you’ll get a lesson designed exclusively for you.

Join the room to begin your lesson

The session feels like a one-on-one language class with a human tutor—but without the high price or time constraints.

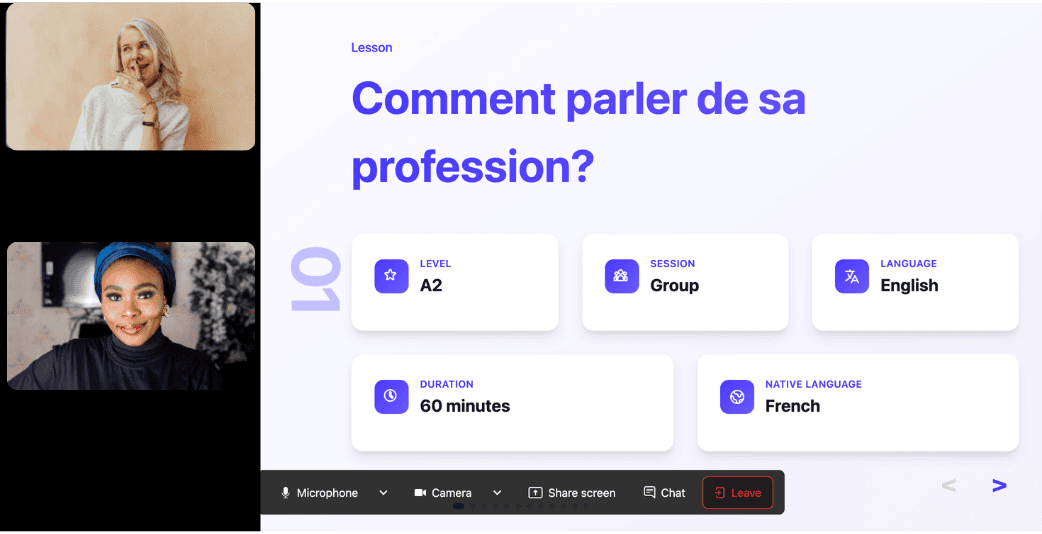
In a 25-minute lesson, Kylian teaches exactly what you need to know about your chosen topic: the nuances that textbooks never explain, key cultural differences between French and your target language, grammar rules, and much more.

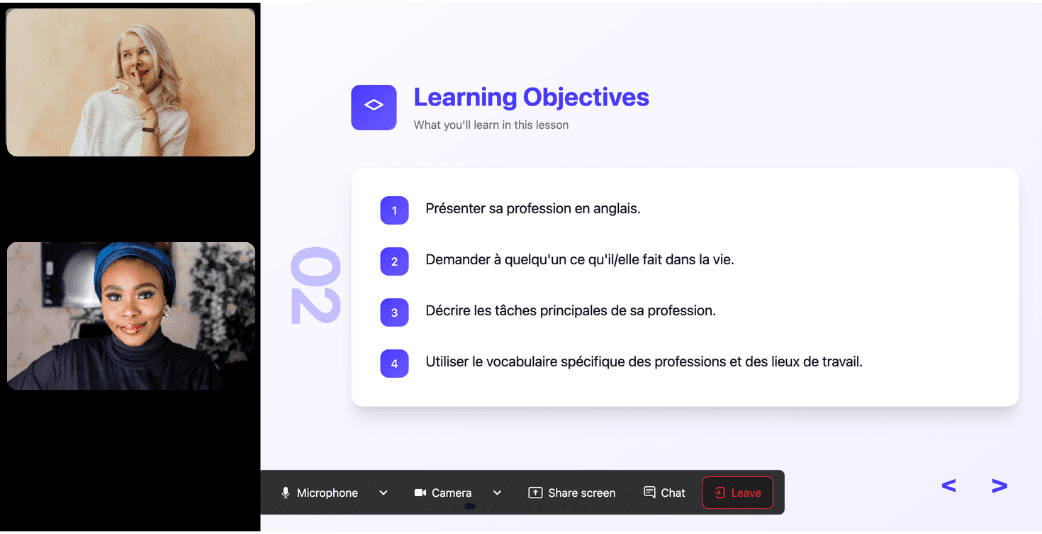
Ever felt frustrated trying to keep up with a native-speaking teacher, or embarrassed to ask for something to be repeated? With Kylian, that problem disappears. It switches intelligently between French and the target language depending on your level, helping you understand every concept at your own pace.

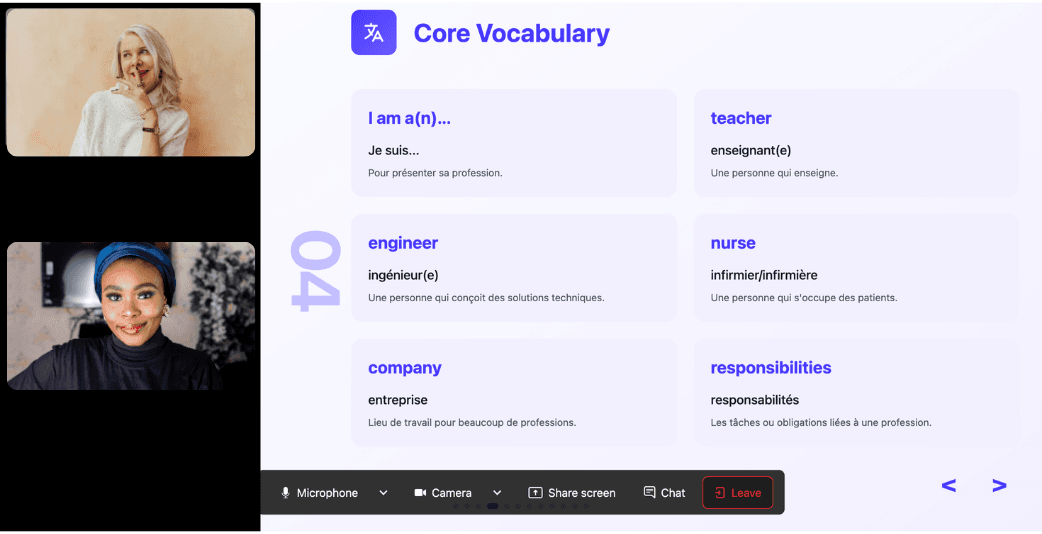
During the lesson, Kylian uses role-plays, real-life examples, and adapts to your learning style. Didn’t understand something? No problem—you can pause Kylian anytime to ask for clarification, without fear of being judged.

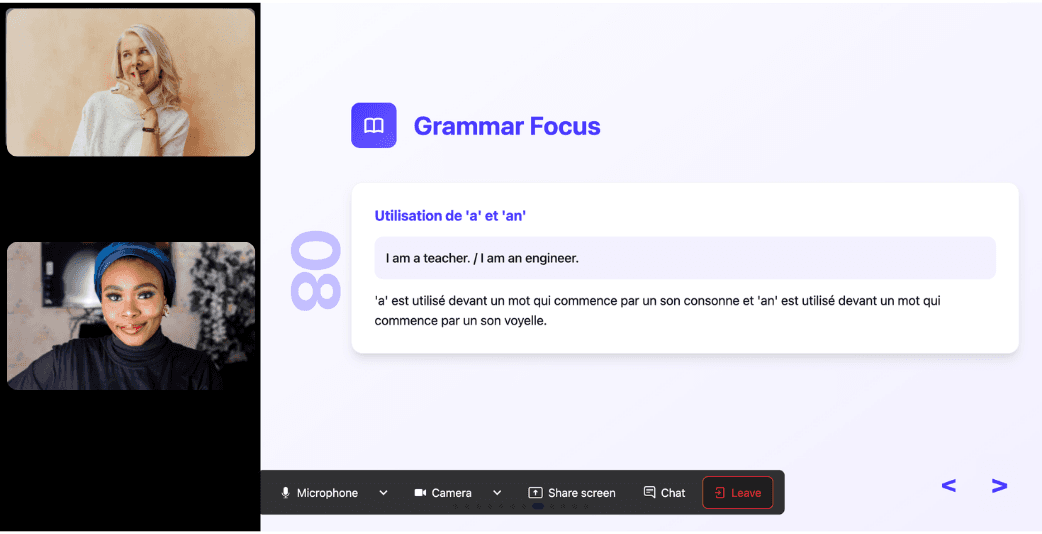
Ask all the questions you want, repeat sections if needed, and customize your learning experience in ways traditional teachers and generic apps simply can’t match.

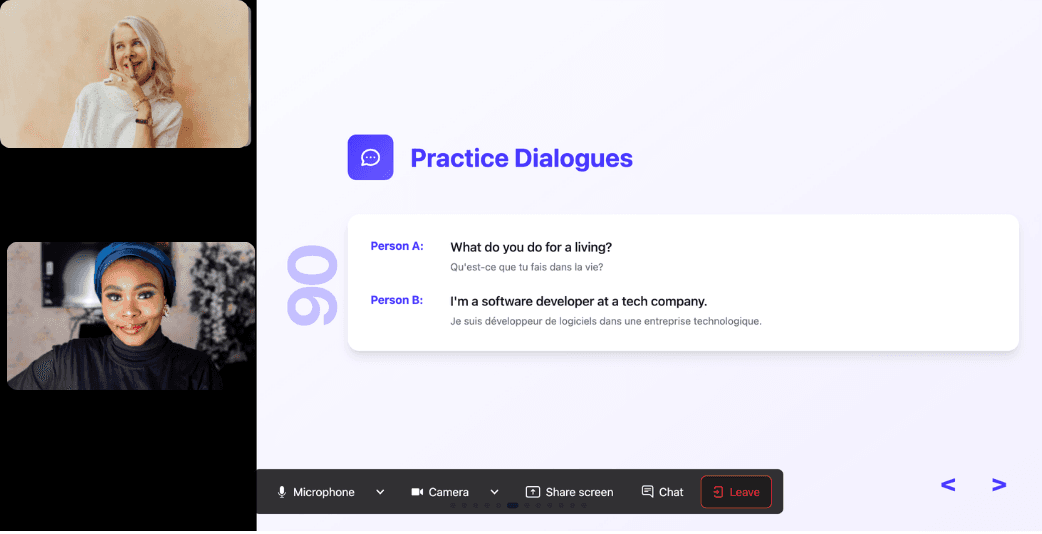
With 24/7 access at a fraction of the cost of private lessons, Kylian removes all the barriers that have kept you from mastering the language you’ve always wanted to learn.